Sesin nasıl modellendiğini bir önceki bölümde anlattım. Bu modelin parametrelerinin ilki, Genlik ile detaya girelim. Hemen ses dalgasının formülünü hatırlayalım:
y(t) = Asin(2πƒt + Φ)
Bu formüldeki A genliğe karşılık geliyor.
Ses basıncının birimi Pascal (pa). Genliği daha önce desibel ile gösteriyoruz dedim ama deciBel bir basınç birimi değil. Daha sonra anlatacağım, şimdilik basınç konusunda kalalım. Basınç birimine bu konuda çalışan Fransız matematik ve fizikçisi Blaise Pascal’ın adı verilmiş.
Önce devamlı maruz olduğumuz atmosfer basıncına bakalım. Üzerimizde 10-12 km yüksekliğinde bir atmosfer var. Hava gittikçe seyrelerek dünyanın üzerinde bizi koruyan ve yaşatan bir kalkan olarak duruyor. Bu kadar havanın ciddi bir basıncı var tabii. Bu basıncın Pascal birimindeki değeri 101,325 pa. Şimdi bu rakam size bir şey ifade etmiyor tabii. Ama ses basıncıyla karşılaştırınca ne kadar büyük bir basınç olduğunu göreceksiniz. Burada beni de çok etkileyen durum duyabildiğimiz en düşük sesin basıncı, ya da bu atmosferik basıncın üzerinde oluşturduğu ekstra titreşimin basıncı. Yani ses dediğimiz şey 101,325 pa olan atmosferik basıncın azıcık artması ve azıcık azalmasından oluşan bir titreme. Biz o basınç farklılığını duyuyoruz. Bu titreşimin oluşturduğu basınç farklılığına Ses Basınç Seviyesi (Sound Pressure Level) adı veriliyor. Kısaltması SPL.
Şimdi ilginç nokta geliyor: Duyabildiğimiz en düşük sesin basınç farklılığı 0.00002 pa. Yani toplam atmosferik basıncın 5 milyarda biri boyunda titreşimleri duyabiliyoruz. Tabii bu küçüklükteki bir titreşimi ancak sessiz odada bir süre kalıp sessizliğe alıştıktan sonra duyabiliyoruz, o ayrı. Fakat minimum değer sessiz odalarda yapılan deneylerde böyle çıkmış. Normal hayatta minimum duyabildiğimiz seviye daha yüksek zira ortam gürültüsü bu sesleri maskeliyor ve kulağımız bu gürültüyü filtreliyor.
Öte yandan işitme duyumuza zarar verecek kadar yüksek ses basıncı seviyesi de 200 pa. Düşününce, duyabildiğimiz en yüksek basınçlı titreşimle en düşük arasındaki fark 10 milyon kat, inanılmaz genişlikte bir aralık.
Bu iki sınır arasındaki basınç seviyelerini günlük yaşamımızdan örneklerle dolduralım:
| SPL (pa) | Açıklama |
| 0.00002 | Teorik sınır |
| 0.0002 | Sessiz ortam |
| 0.002 | Sessiz ev ortamı |
| 0.02 | Normal konuşma |
| 0.2 | Klasik müzik konseri |
| 2 | Disko, caz konseri |
| 20 | Rock konseri – acı eşiği |
| 200 | Zarar verme eşiği |
Bu değerleri bir grafikte göstermek istersek, kabaca şöyle oluyor:
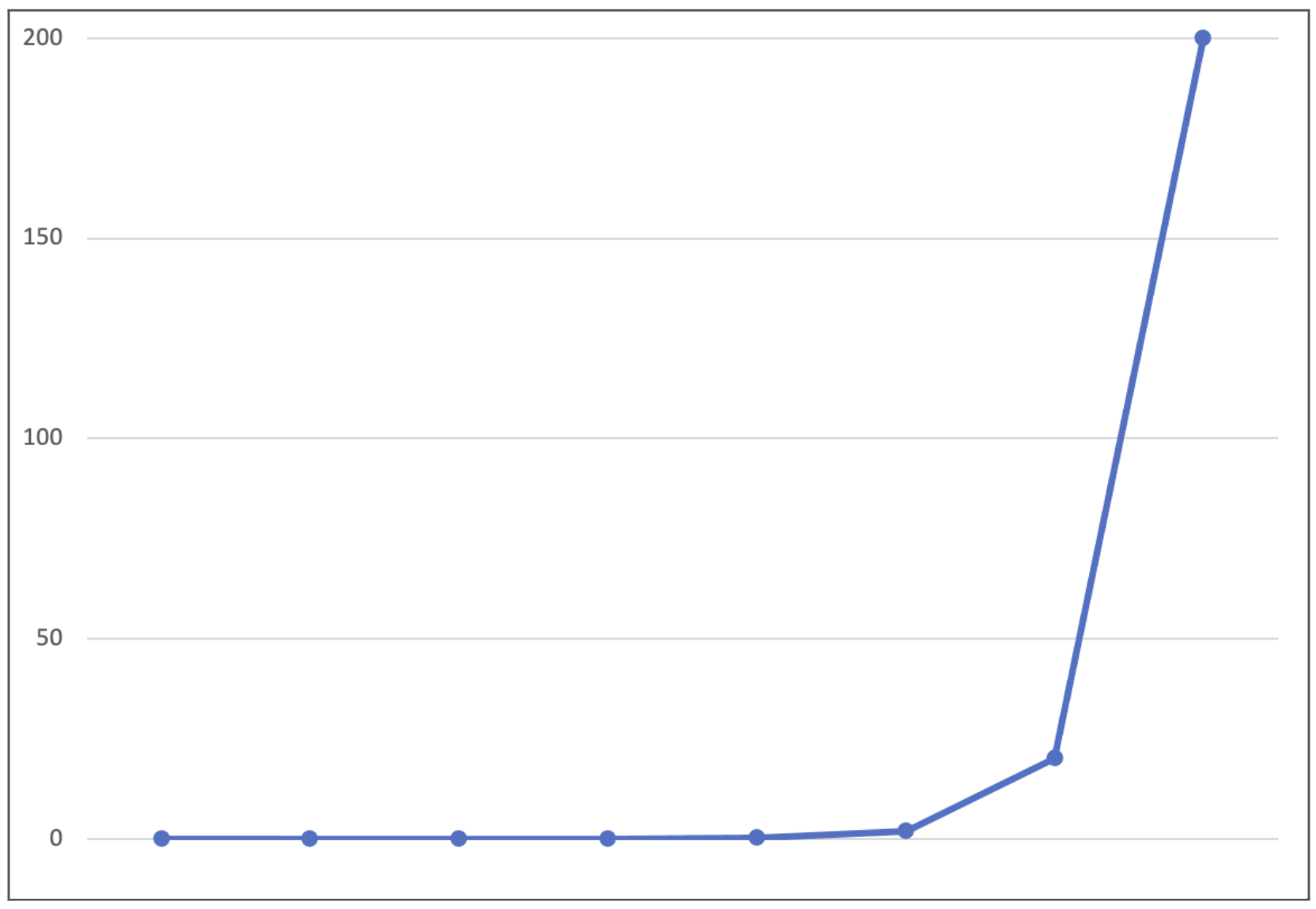
Gördüğünüz gibi pek güzel bir grafik değil, son iki değere kadar bütün değerler neredeyse birinin aynıymış gibi görünüyor. Oysa ki, günlük yaşamdaki algılanışları çok farklı. Öte yandan bu basınç değerleri hatırlanabilecek sayılar değil. Sessiz ev ortamı nokta sıfır sıfır iki miydi, nokta sıfır iki miydi hatırlamak zor. Bu nedenle Pascal birimi sesle ilgili seviyeyi yani genliği tanımlamak için iyi bir birim değil o yüzden başka birim kullanmak gerekiyor.
Doğrusal ve Logaritmik Değerler Ne Demektir?
Başka bir birim derken ne demek istiyoruz? Doğada rastladığımız olguların değişim biçimi genelde iki şekilde oluyor: Doğrusal ya da logaritmik. Doğrusal eklenerek ya da çıkarılarak değişen, logaritmik çarpılarak ya da bölünerek değişen değerler. Örnekler verelim:
Doğrusal:
- Örneğin 10, 20, 30, 40 gibi 10 eklenerek artma
- Hız – yol
- Voltaj – Akım
Logaritmik:
- Örneğin 1, 10, 100, 1000 gibi 10‘la çarpılarak artma
- Salgın hastalığın yayılma hızı
- Deprem şiddetini belirleyen Richter ölçeği
- Güç – ses yüksekliği
Ses basıncı algımız yapısı gereği çarpılarak büyüyen bir doğal olgu. Örneğin basınç on misline arttığında işitme duyumuz sanki kabaca iki misli artmış gibi duyuyor.
Logaritma genel olarak 10’un katları üzerinden hesaplanıyor. 1’in logaritması sıfır. 10, 100 gibi sayıların logaritmasını bulmak için kaç sıfırı olduğuna bakıyoruz. Eğer değerler 1’den küçükse o zaman logaritması eksi oluyor. Birkaç örnek verelim:
- Log 1000 = 3
- Log 100 = 2
- Log 10 = 1
- Log 1 = 0
- Log 0.1 = -1
- Log 0.01 = -2
- Log 0.001 = -3
1000 ile 100 arasında kalan sayıların logaritmaları da 3 ile 2 arasında oluyor. Logaritmanın güzelliği doğada ses basıncı gibi logaritmik olarak değişen değerlerin logaritmasını alınca onları doğrusal hale getirmemiz. Biraz kafa karıştırıcı ama sese uyguladığımızda daha iyi anlaşılacak. O yüzden pes etmeyin…
Desibel Tanımı
Ses algımız logaritmik şekilde çalıştığı için sayıları hatırlayabilmek ve daha rahat anlamlandırabilmek ve hatırlamak için değerlerin logaritmasını alıp onları doğrusal hale getirmek çok daha kullanışlı bir yöntem.
Bu yöntemi ilk defa Alexander Graham Bell telefon sistemlerinde ses seviyesini göstermek için kullanmış. Sonrasında gelen kişiler bu birime onun adını vermişler (arada bir L harfi atılmış tabii). İlk kullanımında adı Bel olmuş ama sayılar biraz küçük kalınca onun 10 misli olan desibel birimi standard olmuş. Bel ve desibel arasındaki fark metre ile desimetre arasındaki fark gibi. 1 Bel, 10 desibel’e karşılık. Kısaltılması dB şeklinde yazılıyor.
Ses basıncı için şöyle hesaplanıyor:
- Duyabildiğimiz en düşük seviyeyi temel alıyoruz. Buna P0 deniyor.
- P0 = 0.00002 pa
- Değerini desibel olarak belirtmek istediğimiz seviyeye P diyelim. Bu seviyenin temel aldığımız en düşük seviye ile oranını hesaplıyoruz:
- P / P0
- Bunun da logaritmasını alınca bir anda doğrusal bir birime kavuşuyoruz.
- log (P / P0)
- Eğer oranını aldığımız değerler güç değil de basınç, gerilim, akım gibi değerlerse bu oranı 2 ile çarpıyoruz (Bunun nedeni çok önemli değil ama merak edenler için ileride açıkladım).
- 2 * log (P / P0)
- Şu anda Bel olarak değeri bulduk. Fakat daha kullanışlı olduğu için 10’la çarpıp desibel’e çevirmek uygun gelmiş.
- 20 * log (P / P0)
- Bu çıkan değer bize en düşük seviyeye göre doğrusal hale getirilmiş bir seviye veriyor.
Bu değeri daha önce belirttiğimiz ses basıncı seviyeleri için hesapladığımızda çıkan sayılar şöyle:
| SPL (pa) | dBSPL | Açıklama | Oran |
| 0.00002 | 0 | Teorik sınır (P0) | 1 |
| 0.0002 | 20 | Sessiz ortam | 10 |
| 0.002 | 40 | Sessiz ev ortamı | 100 |
| 0.02 | 60 | Normal konuşma | 1,000 |
| 0.2 | 80 | Klasik müzik konseri | 10,000 |
| 2 | 100 | Disko, caz konseri | 100,000 |
| 20 | 120 | Rock konseri – acı eşiği | 1,000,000 |
| 200 | 140 | Zarar verme eşiği | 10,000,000 |
Örneğin sessiz ev ortamı için hesaplama şöyle yapılıyor:
20 * Log(0.002 / 0.00002) = 40 dB
Her şeyden önce bu dB değeri çok daha akılda kalıcı bir sayı. Ayrıca doğrusal bir şekilde ilerliyor. Grafiğini çizdiğimiz zaman daha rahat anlaşılır ve değerlendirebilir bir grafik çıkıyor:
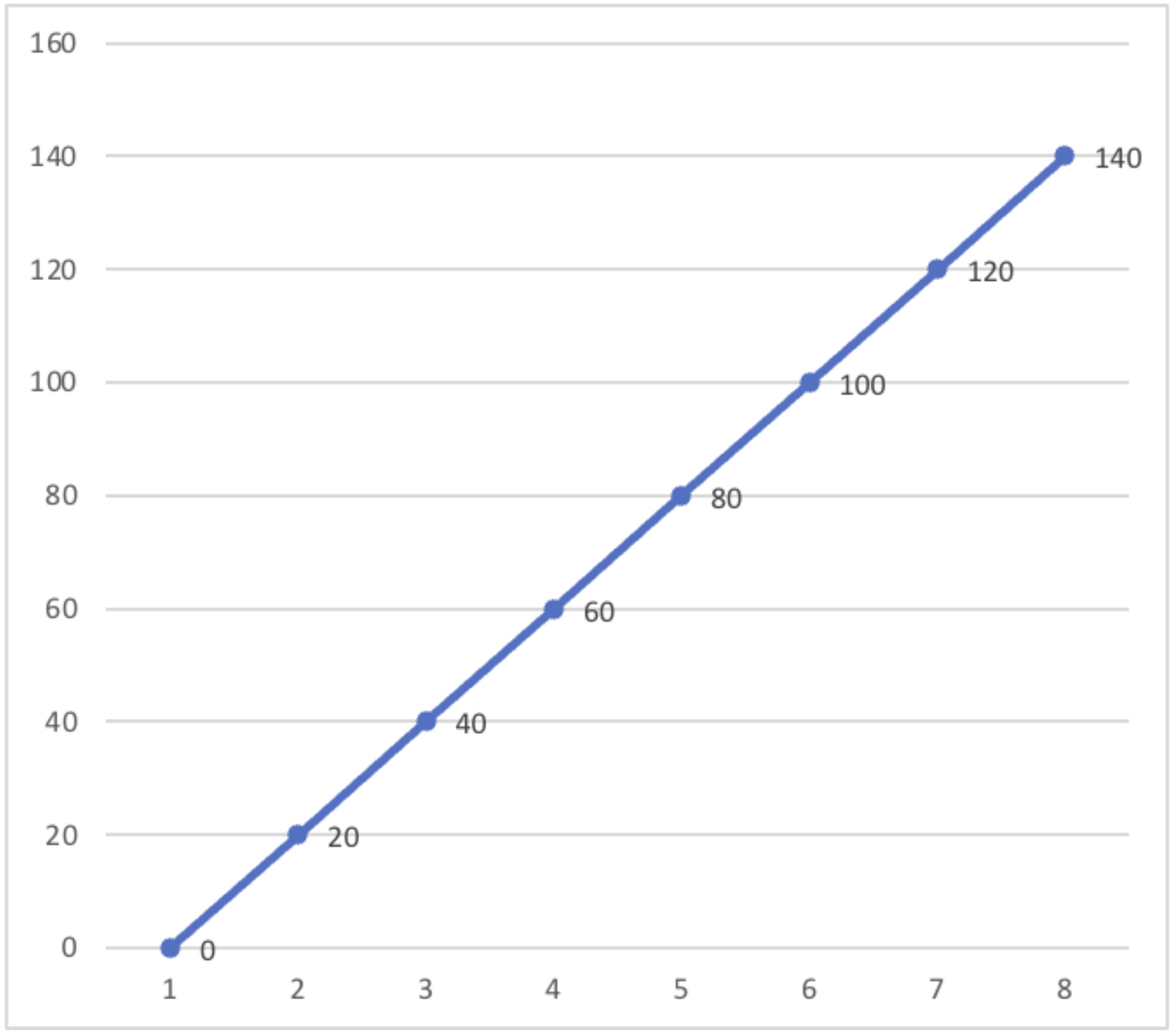
Logaritma ve desibel sayesinde arasındaki fark 10 milyon misli olan bir değeri algıladığımız biçime yakın, grafiklerde kolay gösterilebilir ve tam sayı olduğu için kolay hatırlanabilir bir birime çevirmiş olduk. Bu nedenlerle desibel çok kullanışlı bir birim.
Ses basıncı (SPL, pa) ya da gerilim (Volt) değerleriyle onların desibel gösterimi arasındaki değişim farklarına bir kaç örnek yararlı olacaktır:
- +6 dB = 2 misli ses basıncı (SPL) ya da gerilim (Volt)
- +20 dB = 10 misli ses basıncı (SPL) ya da gerilim (Volt)
- +40 dB = 100 misli ses basıncı (SPL) ya da gerilim (Volt)
- +60 dB = 1,000 misli ses basıncı (SPL) ya da gerilim (Volt)
- +80 dB = 10,000 misli ses basıncı (SPL) ya da gerilim (Volt)
Benzer bir şekilde desibel değeri eksi olduğunda bu sefer değer bölünüyor:
- -6 dB = Ses basıncı (SPL) ya da gerilimin (Volt) yarısı
- -20 dB = Ses basıncı (SPL) ya da gerilimin (Volt) 10’da biri
- -40 dB = Ses basıncı (SPL) ya da gerilimin (Volt) 100’de biri
- -60 dB = Ses basıncı (SPL) ya da gerilimin (Volt) 1000’de biri
- -80 dB = Ses basıncı (SPL) ya da gerilimin (Volt) 10000’de biri
Desibel’in Oran Olarak Kullanımı
DesiBel hesaplama yönteminin çok kullanışlı olduğu bir başka kullanımı daha var, oran olarak kullanımı. Aslına bakarsanız SPL hesaplamak için de ilgilendiğimiz değerin P0’a oranını hesaplamıştık. Bu yöntemle sesin genliği dışındaki zor hatırlanır oransal değerleri de desiBel ile göstermek mümkün.
Örneğin bozulma – distortion
- %1 = 20 * log (1/100) = -40 dB
- %0.1 = 20 * log (1/1000) = -60 dB
- %0.01 = 20 * log (1/10000) = -80 dB
Ya da Sinyal – Gürültü Oranı (Signal to Noise Ratio – SNR)
- 20 * log (sinyal seviyesi / gürültü seviyesi)
Bu hesaplama yöntemi çok kullanışlı. Eğer ses basıncındaki seviye farklılıkların nasıl duyulduğunu biliyorsak o zaman desiBel kullanarak yaptığımız oransal hesaplama bize o değerin nasıl algılandığını da kolaylıkla göstermiş oluyor. Bu hesaplamalara birkaç örnek verelim:
Bozulma (Distortion)
Bir sistemden aldığımız sesin içinde %1 bozulma olduğunu varsayalım. %1 seviye -40 dB’ye karşılık geliyor. Bu durumda bozulmanın seviyesi, ses seviyesinin 40 dB altında olduğunu çok rahatlıkla anlayabiliriz. Evde dinleme seviyemizin 80 dBSPL olduğunu varsayarsak, bu durumda bozulmanın seviyesi 40 dBSPL seviyelerinde olacak demektir. Bu da dikkatle dinlendiğinde bu seviyede bir bozulmanın rahatlıkla duyulacağı anlamına gelir.
Gürültü seviyesi (SNR)
Benzer bir şekilde bir sistemin SNR’si 90 dB ise, sesi ancak 90 dBSPL’in üzerinde açtığınız zaman duyulabilir hale geleceğini anlayabiliriz.
SINAD
Toplam harmonik bozulma (Total Harmonik Distortion – THD) ve gürültü seviyesinin birleştirilmiş haline THD+N ismi veriliyor. Bu bir elektronik bileşenin ya da sistemin bozulma ve gürültü profilini basit bir şekilde gösteriyor. Bu değer genel olarak <0.005% gibi verilir. Hatırda kalması ve karşılaştırması zor bir değer. Oysa bunu dB’ye çevirince çok daha anlamlı oluyor. 0.005% THD+N değerinin SINAD karşılığı 86 dB örneğin. Bunu anlamlandırmak çok daha kolay.
- CD için dinamik alan teorik olarak kabaca 96 dB. Eğer bir amfinin SINAD’ı yukarıda hesapladığımız gibi 86 dB ise CD’nin teorik sınırına göre sadece 10 dB daha kötü demektir. Bu da bir amfi için gayet iyi bir değer.
- Benzer bir şekilde, yukarıdaki SPL tablosuna bakarak işitme duyumuzun normal hayatta çalıştığı alan kabaca 20 dBSPL ile 120 dBSPL aralığında yani 100 dB genişliğinde diyebiliriz. Bir DAC için SINAD 100’ün üzerindeyse, gürültü ve bozulma açısından şeffaftır demek mümkün.
Amfi Kazancı (Gain)
Bir başka kullanım da amfilerin kazancının ses seviyesine etkisini hesaplarken kullanılıyor. Örneğin bir güç amfisinin kazancı 26 dB. Bu amfiye giren ses seviyesinin 26 dB yükseldiğini söylüyor bize. -90 dB seviyesinde bir gürültü bu amfiden geçince 64 dB’ye çıkar mesela.
Desibel Bir Birim Midir?
Desibel’i aslında bir birim değil, bir yöntem olarak düşünebilirsiniz. Anlattığımız gibi logaritmik bir genlik değerini bir baz değere göre oranlayıp doğrusal hale getirmek için kullanılıyor. Bu nedenle desibel değerini tek başına belirtmek yetmiyor. Gerçekte hangi değeri belirttiğini söylemek gerekiyor. Yukarıda ses basınç seviyesini (SPL) desibel olarak ifade ettik. Bu durum desibelin kısaltması dB’nin yanına alt metin olarak neyi ifade ettiğini dBSPL olarak yazıyoruz.
Referans olsun diye sık kullanılan değerleri burada özetlemek iyi olur diye düşünüyorum:
| Simge | Açıklama | 0 dB – Baz değer |
| dBSPL | Ses basınç seviyesi – Sound Pressure Level. | 0.00002 pa |
| dBu | Gerilim (Volt) – “unloaded”. 600 Ohm yükte 1 miliWatt gğç harcamak için gereken gerilim. | 0.775 VRMS |
| dBV | Gerilim (Volt) | 1 VRMS |
| dBFS | Sayısal eşdeğer. Kabaca bit başına 6.02 dB geliyor. Örneğin 16 bitlik CD çözünürlüğü kabaca 96 dB’lik bir dinamik alan veriyor. | Bir sayısal sesi örnekleme çözünürlüğünün (bit depth) en yüksek olduğunda eriştiği değer. Örneğin CD için bu değer 0 ile -96 dBFS arasında. |
| dBm | Güç (miliwatt). Dikkat bu sayı hesaplanırken logaritması 10’la çarpılıyor. | 1 mW |
Bir de vintage aletlerde olan VU metrelerle ilgili bir bilgi paylaşayım hazır yeri gelmişken. VU kısaltması Volume Unit’ten geliyor.
Bu göstergelerde dBVU skalası kullanılıyor. 1 kHz’lik bir sinyalin gerilimi +4 dBu yani 1.23 Volt olduğunda ibre 0 dBVU sayısını gösteriyor.
Son Bir Detay
Merak edenler için bu 10 ya da 20’yle çarpma konusunu anlatacağım demiştim. O yüzden son olarak da desibel’in gerilim (volt) ile güç (watt) göstermek için kullanımı arasındaki farka dikkat çekmek istiyorum. Desibel ilk çıktığında bir güç oranı birimi olarak kullanılmış. Yani bir güç değerinin, baz olarak alınan başka bir güç değerine oranı şeklinde. Formülü şu:
- dBgüç = 10 * log(W / W0)
Bu formüldeki 10’la çarpma Bel’den desibel’e çevirmek için. Bu formülü gerilim, basınç gibi değerlere uyguladığımızda onları güç skalasına çevirmemiz gerekiyor. Gerilimin karesi güçle doğrusal orantılı. O yüzden aslında formül şöyle:
- dBgüç = 10 * log (V2 / V02)
Buradaki kareleri dışarı aldığımızda formül basitleşiyor.
- dBgüç = 20 * log (V / V0)
O yüzden bir değeri desibel’e çevirirken bunun bir güç değeri olup olmadığına bakarak 10 ya da 20 ile çarpmak gerekiyor.
Bu bölümün sunum kaydı: https://youtu.be/0OO0qbKE0Tw?si=bNsjUy-s-HiafPFM
